Bouquet of Circles

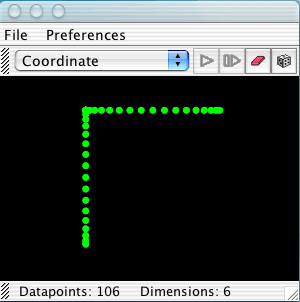
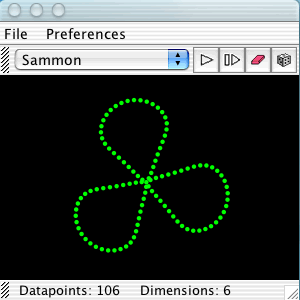
A bouquet of circles is an arbitrary number of circles joined a single point. This is a bouquet of three circles sitting in a six-dimensional space. In a six dimensional space, three mutually perpendicular planes can meet at a single point. Each of the circles in this bouquet sits in its own plane which is perpendicular to the other two. Shown here are three projections of the bouquet of three circles.

On the left is a coordinate projection of the bouquet. Two of the circles are seen side-on, and one is being projected straight on to the intersection point. In the center, the bouquet is projected on to its principle axes, which are the axes around which the points of the dataset are most "balanced." This allows all three circles to be seen side-on, in a way which makes the symmetry of the figure evident. We can see that the angle between any two of the circles is the same. On the right is a Sammon mapping of the bouquet. Now we are able to see the actual topology of the figure, along with its symmetry.

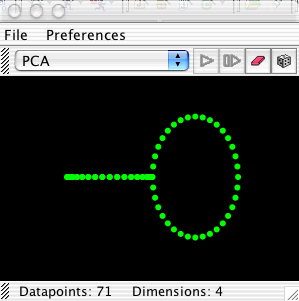
A figure eight space is a special kind of bouquet of circles comprising two circles joined at single point. It is called a figure eight space because it resembles the numeral "8". A figure eight space has a nice shape in a four dimensional space. In four dimensions two perpendicular planes can intersect at a single point. A circle can be placed in each of the planes so that they meet at the intersection point. This way the two loops of the figure eight space are perpendicular to each other.

This figure eight space has been projected down to two dimensions using PCA and the Sammon map. The result using the PCA is shown on the left below and the result using PCA is shown below on the right. Away from the intersection point the circular shape of the loops is preserved. However at the intersection point the loops have been straightened out to better show how fast the distance between the two circles increases as we move away from the intersection point.

Here we see the same figure eight space, sampled with fewer points, under the same projections. Note the differences in the corresponding figures. In the figure on the left below, the fact that the circles are perpendicular is preserved. (The difference in the figure is due to the fact that a tie between equal eigenvalues has been broken differently in the two cases).

In a ten dimensional space five mutually perpendicular planes can meet at a single point. A circle can be placed in each of the five planes so they intersect at the intersection point of the five planes. This gives us a bouquet of circles with five loops. On the right is the image of this bouquet of circles projected into a plane using the Sammon map. In the ten dimensional space the bouquet of circles has five fold rotational symmetry which is preserved in the projected image.

The paths followed in a forty dimensional state space of a neural net program, Simbrain, have been projected into a plane using the Sammon map. The projected image is shown on the left. HiSee allows us to see that the paths followed by the neural net in this forty dimensional space form a bouquet of circles with four loops.

We have an elegant figure to the right. In eight dimensional space four mutually perpendicular planes can intersect in a single point. Each of these four planes contains a pair of circles that form a figure eight space. The four figure eight spaces meet at a single point.This is not, strictly speaking, a bouquet of circles, but we can think of it as a bouquet of figure-eights. The symmetry and overall geometry is preserved in the projected image. Each figure eight space is congruent to the others. The two circles in each of the figure eight spaces in this object meet tangentially (unlike the figure eight space above). The four figure eight spaces are perpendicular to each other at their common point.